Mastering Floating Point Formats

The floating-point formats are introduced to represent the floating-point numbers in the computer system. The most widely used floating-point format is the IEEE 754 standard, introduced in 1985. The IEEE 754 standard defines the formats for representing floating-point numbers, the operations on these numbers, and the exceptions that can be raised during the operations. In the original IEEE 754 (1985) standard, the single precision (32-bit) and the double precision (64-bit) floating-point formats are defined. Later on, the standard was revised in 2008, the half precision (16-bit), the quadruple precision (128-bit) and octuple precision (256-bit) floating-point formats were introduced.

With the application of artificial intelligence and the invention of dedicated hardware such as TPU, new floating-point formats are introduced together with the AI-oriented hardware, like the bfloat16, the tensor float 32, etc. To be short, the major difference between different floating-point formats is the exponent digits and fraction digits, which decide the precision and the range of the floating-point numbers.

The standard IEEE 754 floating-point formats

The single precision (32-bit) and the double precision (64-bit) floating-point formats are defined in the original IEEE 754 standard. The half precision (16-bit), the quadruple precision (128-bit), and octuple precision (256-bit) floating-point formats are defined in the revised IEEE 754 standard.

• Single Precision (32-bit)

  • 1 bit for the sign
  • 8 bits for the exponent
  • 23 bits for the fraction
  • Range: 1.4E-45 to 3.4E+38
  • Precision: 7 decimal digits

• Double Precision (64-bit)

  • 1 bit for the sign
  • 11 bits for the exponent
  • 52 bits for the fraction
  • Range: 5.0E-324 to 1.7E+308
  • Precision: 16 decimal digits

• Half Precision (16-bit)

  • 1 bit for the sign
  • 5 bits for the exponent
  • 10 bits for the fraction
  • Range: 6.0E-08 to 6.5E+04
  • Precision: 3 decimal digits

• Quadruple Precision (128-bit)

  • 1 bit for the sign
  • 15 bits for the exponent
  • 112 bits for the fraction
  • Range: 6.5E-4966 to 1.1E+4932
  • Precision: 34 decimal digits

• Octuple Precision (256-bit)

  • 1 bit for the sign
  • 19 bits for the exponent
  • 236 bits for the fraction
  • Range: 2.2E-78984 to 1.6E+78913
  • Precision: 71 decimal digits

	single	double	half	quadruple	octuple
sign	1	1	1	1	1
exponent	8	11	5	15	19
fraction	23	52	10	112	236
range-min	1.4E-45	5.0E-324	6.0E-08	6.5E-4966	2.2E-78984
range-max	3.4E+38	1.7E+308	6.5E+04	1.1E+4932	1.6E+78913
precision	7	16	3	34	71

Other floating-point formats

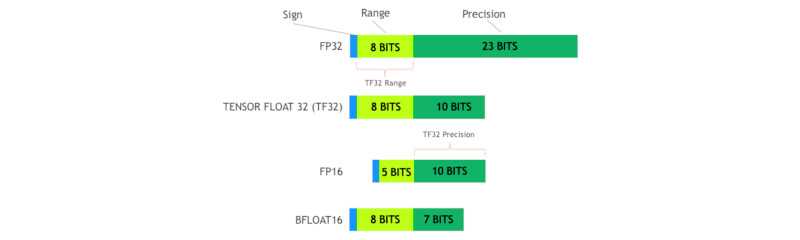
The bfloat16 (16-bit) is introduced by Google, it keeps a similar range as the single precision (32-bit) floating-point format, but with a much smaller precision. The tensor float 32 (32-bit) is introduced by NVIDIA, it also keeps a similar precision as the single precision (32-bit) floating-point format, but extend the precision to be as same as the half precision (16-bit). Both these new formats are introduced to improve the performance of the AI applications.

• bfloat16 (16-bit)

  • 1 bit for the sign
  • 8 bits for the exponent
  • 7 bits for the fraction
  • Range: 9.2E-41 to 3.3E+38
  • Precision: 2 decimal digits

• tensor float 32 (32-bit)

  • 1 bit for the sign
  • 8 bits for the exponent
  • 10 bits for the fraction
  • Range: 1.1E-41 to 3.4E+38
  • Precision: 3 decimal digits

	single	bfloat16	tensor float 32	half
sign	1	1	1	1
exponent	8	8	8	5
fraction	23	7	10	10
range-min	1.4E-45	9.2E-41	1.1E-41	6.0E-08
range-max	3.4E+38	3.3E+38	3.4E+38	6.5E+04
precision	7	2	3	3