Big Changes in the Small World

A Small World is inspired by the concept of “six degrees of separation,” which suggests that any two people on Earth are, on average, six or fewer social connections apart. In graph theory, a small-world network is characterized by a high clustering coefficient and short average path lengths between nodes. To get more insights into small-world networks, we can refer to the Watts Strogatz Model, which is a mathematical model that generates graphs with small-world properties.

On top of the small-world concept, we have a problem to solve: similarity search in high-dimensional spaces. Similarity Search is a common task in various applications, such as image retrieval, recommendation systems, and natural language processing. The goal is to find the most similar items to a given query item based on a defined similarity metric. The state-of-the-art solution to this problem is the Hierarchical Navigable Small World (HNSW) algorithm. HNSW is designed to efficiently find approximate nearest neighbors in high-dimensional spaces by leveraging the properties of small-world networks.

Basic Concepts

Nearest Neighbor Search

Nearest Neighbor Search is a fundamental problem in machine learning and data mining, where the goal is to find the closest data points (neighbors) to a given query point based on a defined distance metric (e.g., Euclidean distance).

Skip Lists

Skip Lists are a probabilistic data structure that allows for fast search, insertion, and deletion operations by maintaining multiple levels of linked lists. The data in skip lists is organized in layers, where each higher layer acts as an “express lane” for the lower layers, enabling quicker traversal through the list.

How HNSW Works

Graph Construction

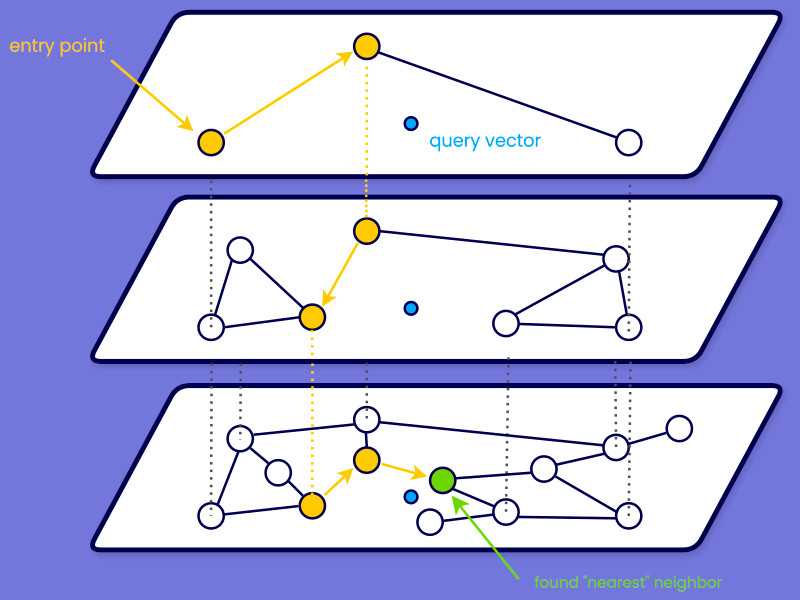
• Layers: The HNSW structure consists of several layers, with the bottom layer containing all data points and higher layers containing a subset of these points. The topmost layer has the fewest points, facilitating quick navigation.
• Connections: Each node in a layer is connected to a limited number of nearest neighbors within that layer. The connections are established based on a distance metric, ensuring that nodes are linked to their closest counterparts.
• Entry Point: The search process begins at the topmost layer, where the entry point is typically a randomly selected node. From there, the algorithm navigates down through the layers to find the nearest neighbors in the bottom layer.

Algorithm

• Insert: When a new data point is added to the HNSW structure, it is assigned to a random layer based on a probabilistic distribution. The point is then connected to its nearest neighbors in that layer, and the connections are updated accordingly.
• Search: The search algorithm starts at the entry point in the top layer and navigates through the graph by moving to the nearest neighbor nodes in each layer. This process continues until it reaches the bottom layer, where a more detailed search is performed to find the closest neighbors.